Care este derivata a doua ordine

Funcția este complexă, dacă poate fi reprezentat ca o funcție a funcției y = f [φ (x)], unde y = f (u), Au = φ (x) argument gdeupromezhutochny. Orice funcție complexă poate fi exprimată ca funcții elementare (simple), care sunt intermediare argumentele.

funcții simple: Complicații:

y = x 2 y = (x + 1) 2; u = (x + 1); y = u 2;

y = sinx; y = sin2x; u = 2; y = sinu;

y = e x e y = 2, u = 2; y = e u;

Inh y = y = ln (x + 2); u = x + 2; y = LNU.

Regula generală pentru diferențierea unei funcții compozită, având în vedere teorema redusă, fără dovezi.

Dacă funcția u = φ (x) are proizvodnuyuu'x = φ '(x) la punctul x, o funcție y = f (u) derivat u'u = f' (u) în tochkeu respectiv, derivatul compozit funcția y = f [φ (x)], la un punct x este dată de: y'x = f '(u) · u' (x).

Adesea folosit mai puțin precise, dar mai scurt formularea acestei teoreme: derivata unei funcții compozit este produsul unui derivat al unei variabile intermediare derivatei variabila intermediar al variabilei independente.

Exemplu: y = sin2x 2; u = 2 2; y = sinu;

3. Derivat de ordinul al doilea. sens mecanic al doilea derivat.

Derivata funcției y = f (x) se numește un prim ordin derivat sau un derivat al primei funcții. Acest derivat este o funcție de x, și este posibil să se diferențieze din nou. Derivatul derivatului este denumit derivat de ordinul doi sau un al doilea derivat. Este indicat: pagina "x - (y două linii prin X); f" (x) - (ef doua bar dimensional prin X); d 2 y / dx 2 - (te doi y de Te X de două ori); d 2 f / 2 dx - (te doi X eff de două ori).

Pe baza determinării derivata a doua, putem scrie:

Derivata a doua, la rândul său, este o funcție de x, și este posibil să se diferențieze și să obțină un al treilea ordin, etc.

sens mecanic al doilea derivat este explicată pe baza accelerației instantanee, care se caracterizează prin mișcarea alternante.

Dacă S = f (t) - ecuația de mișcare, to = S't; Asr. =

;

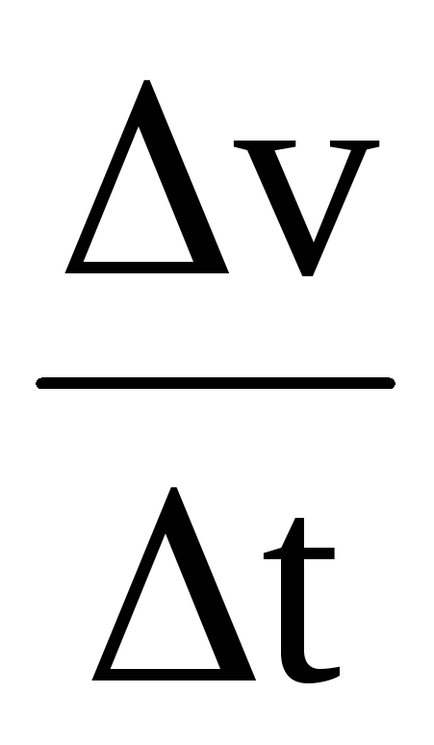
AMGN. =

asr =





= 't; AMGN. = 't = (S't) „t = S„tt.

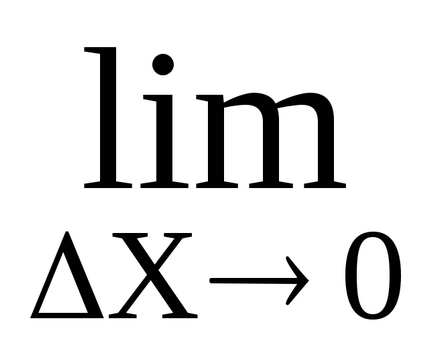
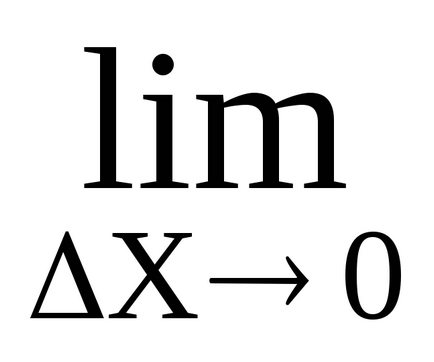
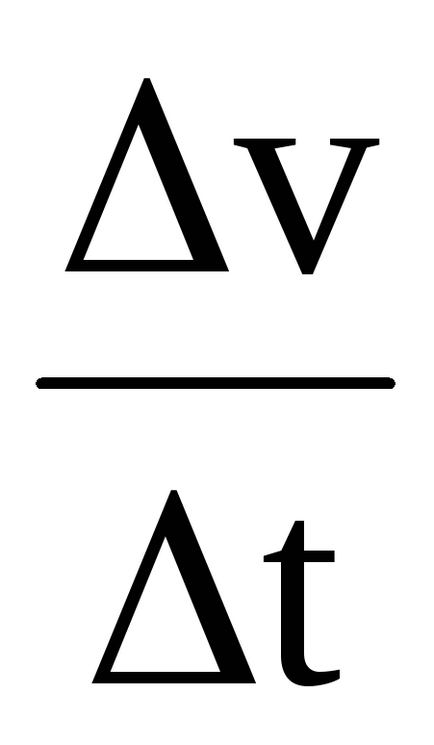
Astfel, derivata a doua a căii în raport cu timpul este egală cu accelerația instantanee a mișcării alternante. Aceasta este fizică (mecanică) sens al doilea derivat.

Exemplu: Fie mișcarea liniară a punctului material are loc zakonuS = t 3/3. Accelerația punctului material este definit ca al doilea derivat S "tt: a = S" tt = (t 3/3) „= 2t.

4. Funcția diferențială.

Cu conceptul de derivat este strâns legată de conceptul de funcții diferențiale, care este de mare utilitate practică.

Funcția f (x) are un derivat

= F „(x);

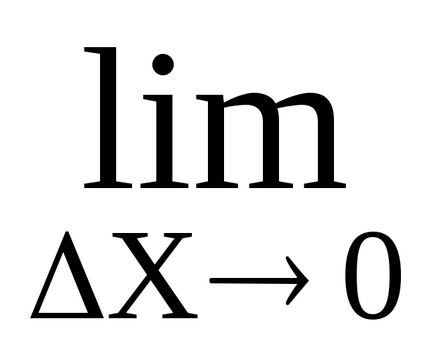
Conform unei teoreme (teorie nu consideră) a conexiunii este valoarea infinit de mici α (AH) (

α (bH) = 0) cu derivatul:= F '(x) + α (bH), unde Δf = f' (x) bH + α (bH) · bH.

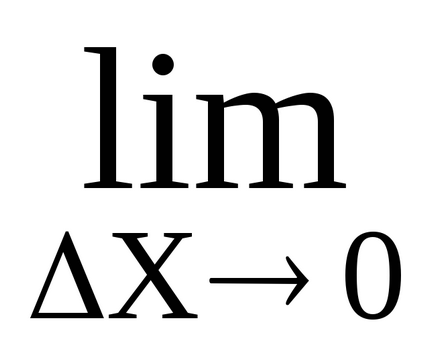
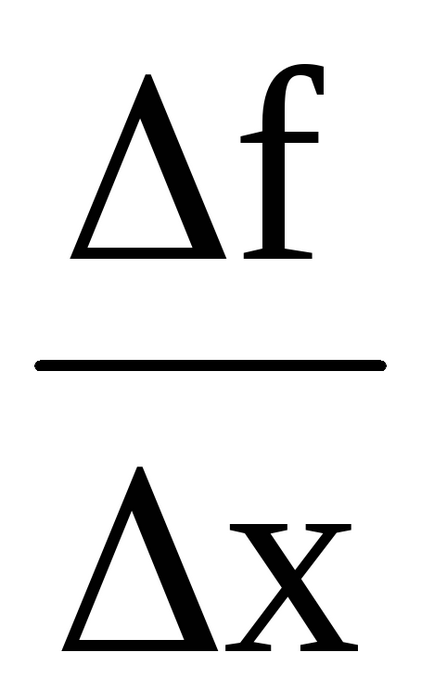
Ultima egalitate implică faptul că incrementarea funcției constă într-o sumă, fiecare termen de care este o cantitate infima atunci când bH → 0.

Definim ordinea de micimea a fiecărei infinitezimal această sumă în ceea ce privește infinitezimal bH:

Prin urmare, f infinitezimal (x) bH și bH au același ordin de mărime.

Prin urmare, o cantitate infima α (bH) bH are un ordin mai mare de micime în raport cu o valoare infinitezimal bH. Aceasta înseamnă că expresiile pentru al doilea mandat Δf a (bH) bH converge rapid la 0 când bH → 0 decât primul termen f „(x) bH.

Acesta este primul termen f „(x) se numește funcția diferențială bH la un punct x. Acesta este notat cu DY (Te y) ilidf (de ef). Astfel, dy = df = f '(x) = f ilidy bH' (x) dx, deoarece differentsialdh egal cu increment argument bH (dacă formuledf = f „(x) dx presupus că f (x) = x, atunci poluchimdf = dx = x'h Ax, nox'h = 1, t.e.dx = bH). Astfel, diferența funcției este produsul acestei funcții pe argumentul diferențial.

sens diferențială analitică este că diferența funcției - este principala parte a creșterii funcțiilor Δf, liniară în raport cu argumentul bH. Funcția Differential diferă de funcția increment infinitezimal α (bH) bH ordin mai mare decât bH. Într-adevăr, Δf = f „(x) bH + α (bH) și bH Δf = df + α (bH) bH; otkudadf = Δf- α (bH) bH.

Exemplu: y = 2x 3 + x 2, dy = dy = u'dh = (2x 3 + x 2) „x dx = (6x 2 + 2) dx.

Neglijând α infinitezimal (bH) bH ordin mai mare decât bH. obține df≈ Δf≈ f „(x) dx adică Funcția diferențială poate fi folosită pentru a aproxima calculul funcției increment, deoarece o diferență în general mai ușor de calculat. Diferențialul poate fi aplicată la calcularea aproximativă a valorii funcției. Să ne cunoscut funktsiyay = f (x) și derivatul său la x. Este necesar să se găsească valoarea funcției f (x + bH) într-un cel mai apropiat punct (x + bH). Pentru aceasta folosiți ecuația aproximativă AU ≈dyili AU ≈f „(x) · bH. Având în vedere că = f AU (x + bH) -f (x), poluchimf (x + bH) -f (x) ≈f „(x) · dx, otkudaf (x + bH) = f ( x) + f „(x) · dx. Formula rezultată rezolvă problema.