Cercetarea în clasa a 10-a în studiul temei - proprietățile unui tetraedru regulat
Planul de pregătirea și desfășurarea de sesiuni:
faza I. pregătitoare:- Repetiție proprietăților cunoscute ale unei piramide triunghiulare.
- Ipoteze despre posibil, nu a considerat anterior, caracteristici ale tetraedru.
- Formarea grupurilor de a desfășura activități de cercetare în conformitate cu ipoteza.
- Repartizarea sarcinilor pentru fiecare grup (ținând cont de dorințele).
- Alocarea responsabilităților pentru atribuirea.
- decizie ipoteză.
- Consultarea cu profesorul.
- Efectuarea de lucru.
- Prezentarea și apărarea ipotezei.
- Student Mesaj „Secretele de piramide mari.“
- Deschiderea remarci de către profesor despre diversitatea speciilor de piramide.
- întrebări de discuție:
- Din ce motive se poate combina piramidă triunghiulară greșită
- Ce intelegem prin orthocenter triunghi, și ceea ce poate fi numit orthocenter tetraedrului
- Există orthocenter în Tetrahedron dreptunghiular
- Ceea ce se numește un tetraedru isohedral ce proprietăți ar putea avea
- Ca urmare a examinării unei varietăți de tetraedre, discuta despre proprietățile lor clarifică conceptele și există o anumită structură:
Proprietăți 1-4 dovedit oral folosind Slayda1.
Proprietatea 1. Toate marginile sunt egale.
2. Toate bunurile unghiurilor plane sunt egale cu 60 °.
Proprietatea 3: Sumele se confruntă cu unghiuri în toate cele trei vârfuri ale unui tetraedru este egal cu 180 °.
Proprietatea 4. Dacă tetraedrul este corectă, atunci orice nod proiectat în fața opusă orthocenter.
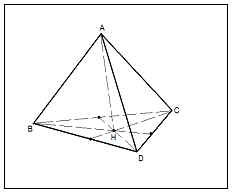
ABCD - un tetraedru regulat
1) punctul H poate coincide cu oricare dintre punctele A, B, C. Fie H? B, H? C
2) AH + (ABC) => AH + BH, AH + CH, AH + DH,
3) Să considerăm ABH, BCH, ADH
AD - ansamblu => ABH, BCH, ADH => BH = CH = DH
AB = AC = AD r H -. ABC este orthocenter
QED.- Prima lecție Proprietățile 5-9 sunt formulate ca ipoteze, care necesită dovezi.
Fiecare grup primește temele sale:
Dovedește una dintre proprietățile.
Se prepară un studiu cu prezentarea.
II. Scena principală (în timpul săptămânii):- decizie ipoteză.
- Consultarea cu profesorul.
- Efectuarea de lucru.
III. Pasul final (1-2 unități):
Reprezentarea și protecția ipotezei cu utilizarea de prezentări.
În pregătirea materialului pentru lecție finală, elevii vin la concluzia că special punctul de intersecție de înălțimi, suntem de acord să-l numim punctul „uimitor“.
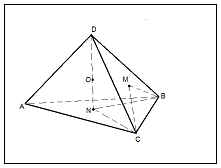
Proprietate 5: centre ale circumscris și sferele inscriptionate coincid.
DABC tetraedru -proper
O1 - centrul sferei circumscris
Despre - centrul sferei înscrise
N - punctul de tangență al sferei inscripționată cu o fațetă a FAA
Să presupunem că OA = OB = OD = OC - razele circumscris
Omit ON + (ABC)
AON = CON - dreptunghiular. catete și prin ipotenuza => AN = CN
Omit OM + (BCD)
COM DOM - dreptunghiular. pe picior și un ipotenuza => CM = DM
De n. 1 CON COM => ON = OM
ON + (ABC) => ON, OM - razele cercului inscris.
Pentru un tetraedru regulat există posibilitatea unui acord reciproc cu sfera - cu o atingere a unei sfere toate coastele. O astfel de domeniu de aplicare este uneori numit „poluvpisannoy“.
Proprietatea este de 6: segmentele care unește punctele de centru margini opuse și aceste margini sunt perpendiculare pe sfera razelor poluvpisannoy.
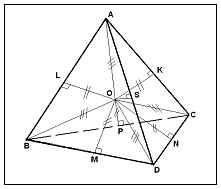
ABCD - un tetraedru regulat;
AL = BL, AK = CK, AS = DS,
BP = CP, BM = DM, CN = DN.
LO = OK = OS = OM = ON = OP
Tetraedru ABCD - dreapta => AO = BO = CO = DO
Luați în considerare triunghiul AOB, AOC, COD, BOD, BOC, OCD.
AO = BO => AOB -? Isosceles =>
OL - mediana, altitudinea, bisector
AO = CO =>? AOC- isoscel =>
OK- mediana, altitudinea, bisector
CO = DO =>? COD- isoscel =>
mediană ON, altitudinea, bisectoare AOB => AOC = COD =
BO = DO =>? BOD- isoscel => BOD = BOC = OCD
Smanului mediana, altitudinea, bisector
AO = DO =>? AOD- isoscel =>
OS- mediana, altitudinea, bisector
BO = CO =>? BOC- isoscel =>
OP- mediana, altitudinea, bisector
AO = BO = CO = DO
AB = AC = AD = BC = BD = CD
3) OL, OK, ON, OM, OS, OP - egal în înălțime OL, OK, ON, OM, sistem de operare, raze OP
triunghiuri isoscele sferă
Într-un tetraedru regulat poate petrece poluvpisannuyu sferă.
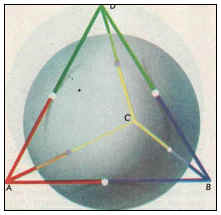
Proprietatea 7: Dacă un tetraedru este corectă, apoi la fiecare două margini opuse ale unui tetraedru sunt reciproc perpendiculare.
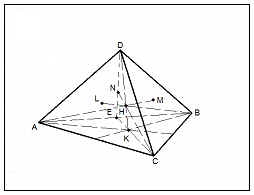
DABC - un tetraedru regulat;
DABC - un tetraedru regulat => ADB -? Echilateral
ED - Înălțimea ADB => ED + AB,
AB + CE, => AB + (EDC) => AB + CD.
au dovedit în mod similar perpendicularitate alte margini.
Proprietatea este de 8: Șase avioane de simetrie se intersectează la un moment dat. Punctul O intersectează patru linii drepte trasate prin centrele cercurilor din jurul fețelor perpendiculare pe planul feței, iar punctul O este centrul sferei.
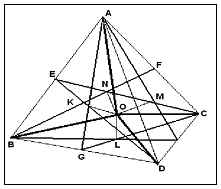
ABCD - un tetraedru regulat
Despre - centrul sferei circumscris;
6 planele de simetrie se intersectează în punctul O;
CG + BD. deoarece BCD - echilateral => GO + BD (teorema de trei perpendicularele GO + BD)
BG = GD, deoarece AG - mediana ABD
ABD (ABD) =>. BOD - isoscel => BO = DO
ED + AB. deoarece ABD -ravnostoronny => OE + AD (circa trei perpendicularele teoremei)
BE = AE, deoarece DE - mediana ABD?
ABD (ABD) => AOB - Isosceles => BO = AO
ON + (ABC) de + AC (timp de aproximativ trei teoremă
BF + AC, ca ABC - perpendicularele echilaterale)
AF = FC, după cum BF - ABC mediana?
ABC (ABC) => AOC - isoscel => AO = CO
BO = AO => AO = BO = CO = DO - raza sferei
AO = CO descris despre ABCD tetraedru
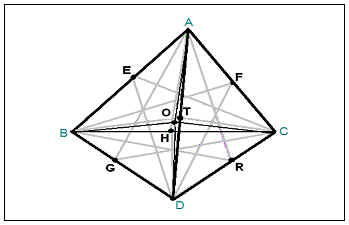
AB + (ABR) (ABR) (BCT) (ACG) (ADH) (CED) (BDF)
Punctul O este centrul sferei circumscris,
6 planele de simetrie se intersectează într-un punct O.
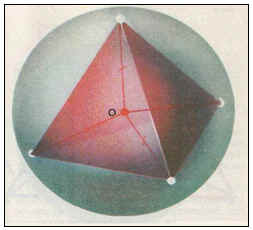
9. proprietate unghi obtuz între perpendicularele care trec prin vârfurile tetraedrul la orthocenter, este de 109 ° 28 '
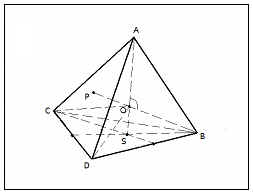
ABCD - un tetraedru regulat;
O - centrul sferei circumscrise;
ASB = 90 o OSB dreptunghiular
2) (pe proprietatea unui tetraedru regulat)
3) AO = BO - razele sferei circumscrise
6) AO = BO = CO = DO =>? OCD =? AOC =? = OCD? COD =? BOD =? BOC
(Prin proprietatea unui tetraedru regulat)
=> = OCD AOC = OCD = COD = BOD = BOC = 109 ° 28 '
Este necesar să dovedească.
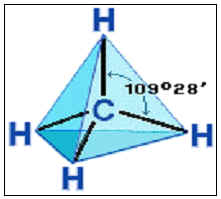
Un fapt interesant este faptul că este acest unghi sunt unele substanțe organice: hidrocarburi și silicați.
Ca rezultat, lucru pe proprietățile unui tetraedru regulat studenților a avut ideea de a apela locul de muncă „punctul Amazing în Tetrahedron“. Au existat propuneri să ia în considerare proprietățile tetraedre dreptunghiulare și isohedral. Astfel, lucrarea a trecut dincolo de domeniul de aplicare al lecției.
- este punctul de intersecție al celor trei axe de simetrie
- este punctul de intersecție al celor șase avioane de simetrie
- este punctul de intersecție al înălțimi ale unui tetraedru regulat
- Acesta este centrul sferei înscrise
- Este centrul sferei poluvpisannoy
- Acesta este centrul sferei
- tetraedru este centrul de greutate
- Acesta este punctul culminant al patru piramide drept egal cu baze triunghiulare - fețele tetraedru.
(Profesor și studenții rezuma lecția. Un scurt raport privind tetraedrului ca unitate structurală a elementelor chimice, efectuate de către unul dintre elevi.)
Proprietățile unui tetraedru regulat și punctul său „uimitor“.
Sa constatat că numai forma tetraedrului având toate proprietățile enumerate mai sus, precum și un punct de „ideal“ poate fi silicați și molecule de hidrocarburi. Sau molecule poate fi compus din mai multe tetraedre regulate. În prezent, tetraedrul este cunoscut nu numai ca reprezentant al vechii civilizații de matematică, dar, de asemenea, ca bază a structurii materiei.
Silicații - Compuși saltlike care conțin compus de siliciu cu oxigen. Numele lor provine de la cuvântul latin „Sileks“ - „Cremene“. Silicați baza moleculara a radicalilor atomice având formă de tetraedre.
Silicații - acest nisip și argilă și cărămidă și sticlă și ciment și smalț, și talc și azbest, și smarald, și topaz.
Silicații compune mai mult de 75% din crusta (și cu circa 87% cuarț) și mai mult de 95% din roci vulcanice.
O caracteristică importantă este abilitatea de a silicaților combinație reciprocă (polimerizare) a două sau mai multe tetraedre siliciu-oxigen printr-un atom de oxigen comun.
Aceste molecule au aceeași formă ca și hidrocarburi saturate, dar ele constau, în contrast cu silicați de carbon și hidrogen. Formula generală a moleculelor
Hidrocarburile includ gaze naturale.
Este necesar să se ia în considerare proprietățile tetraedre dreptunghiulare și isohedral.