Cum se calculeaza aria unui dreptunghi

Care este aria unui dreptunghi, și că o astfel de

Zona - este o astfel de cantitate geometrică, care poate fi utilizată pentru a determina dimensiunea orice suprafață formă geometrică.

Timp de multe secole, astfel încât sa întâmplat calculul zonei numite cuadratură. Asta este, pentru a găsi zona de forme geometrice simple, a fost suficient pentru a contoriza numărul de pătrate de unități, care erau figuri acoperite în mod convențional. O cifră care a avut-o zonă, numită Quadrature.

Prin urmare, este posibil să se rezume că zona - este o astfel de valoare, care ne arată părțile plane de dimensiuni conectate între ele prin segmente.

Dreptunghi - este un patrulater în care toate unghiurile sunt unghiuri drepte. Adică, o formă cu patru laturi, care are patru unghiuri drepte și laturile opuse sunt egale se numește un dreptunghi.

Cum de a găsi aria unui dreptunghi

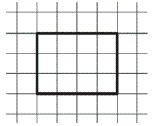
Cel mai simplu mod de a găsi aria unui dreptunghi - pentru a lua o hârtie transparentă, cum ar fi hârtie de calc sau o mușama și raschertit-l în pătrate egale de 1 cm, și apoi atașați la dreptunghiul de imagine. Numărul de pătrate umplute și este zona în centimetri pătrați. De exemplu, figura arată că dreptunghiului se încadrează în 12 pătrate, ceea ce înseamnă că suprafața sa este egală cu - 12 metri pătrați. cm.

Dar pentru a găsi zona de obiecte mari, cum ar fi un apartament, un mod mai universal, formula a fost dovedit astfel încât, în scopul de a găsi aria unui dreptunghi este necesară pentru a multiplica lungimea de lățime.

Acum, să încercăm să găsească zona dreptunghi regula de înregistrare ca formulă. Notăm zona din figura noastre literele S, litera a - reprezintă lungimea, și litera b - lățime.

Ca rezultat, am ajuns aici următoarea formulă:

Dacă aplicați această formulă pentru a figura dreptunghiul de mai sus, vom obține aceleași 12 de centimetri pătrați, ca a = 4 cm, b = 3 cm, și S = 4 * 3 = 12 cmp

Dacă luați două piese identice, și le-a pus una peste alta, ele coincid, și va fi numit egal. Aceste cifre sunt egale ca sunt zone și perimetrul lor.

De ce ar trebui să poată să găsească zona

• În primul rând, dacă știi cum să găsească zona de orice formă, cu ajutorul formulei sale, va fi capabil să rezolve orice probleme în geometria și trigonometria fără probleme.
• În al doilea rând, să învețe să găsească aria unui dreptunghi, mai întâi va fi capabil de a rezolva puzzle-uri simple și în cele din urmă va trece la mai complicate, și va învăța cum să găsească zona de cifre, care sunt înscrise într-un dreptunghi sau în apropierea acestuia.
• În al treilea rând, cunoscând o astfel de formulă simplă ca S = a * b, aveți posibilitatea, fără probleme pentru a rezolva orice sarcini simple de uz casnic (de exemplu, pentru a găsi un apartament S sau casa), și în cele din urmă să fie în măsură să le aplice pentru a rezolva proiecte arhitecturale complexe.

Asta este, dacă într-adevăr simplifica formula pentru a găsi zona, va arata astfel:

Aceasta indică faptul că n - o zonă dorită, A - este lungimea, W - denotă lățimea sa, iar x - este semnul de multiplicare.

Știați că zona oricărui poligon poate fi împărțit într-un anumit număr de blocuri pătrat, care sunt în interiorul acestui poligon? Care este diferența dintre suprafața și perimetrul

Să încercăm un exemplu pentru a înțelege diferența dintre perimetrul și zona. De exemplu, școala noastră este situată într-o zonă care este împrejmuit - lungimea totală a perimetrului gardului va fi, iar spațiul care este situată în interiorul incintei și este pătrată.

Unitatea de suprafață

Dacă perimetrul este măsurat într-un unități liniare unidimensionale, care sunt inch, picioare și m, S se referă la calculul bidimensional și are o lungime și lățime.

Și S măsurată în unități pătrate, cum ar fi:

• Un milimetru pătrat, unde S unui pătrat cu latura egală cu un milimetru;
• centimetru pătrat, o astfel de S are un pătrat a cărui latură este egală cu un centimetru;
• decimetru pătrat este S unui pătrat cu latura de un decimetru;
• squaremeter S are un pătrat a cărui latură este egală cu un metru;
• Și, în sfârșit, un kilometru pătrat are un pătrat S a cărui latură este egală cu un kilometru.

Pentru a măsura zona de zone mari astfel de unități utilizate pe suprafața Pământului, cum ar fi:

• Un AP sau tesut - în cazul în care S este un pătrat cu latura de zece metri;
• Un hectar este egală cu pătratul S, a cărui parte are o sută de metri.

exerciţii

Acum, să ne uităm la câteva exemple.

Figura 62 este desenată figura, care are opt pătrate și fiecare parte a acestor pătrate este egală cu un centimetru. Prin urmare, această S pătrat este centimetru pătrat.

În cazul în care înregistrarea, se va arata astfel:

1 cm2. Și toate această cifră S compusă din opt pătrate va fi de 8 cmp

Dacă luați orice bucată și rupe-l în jos în pătrate „p“ cu laturile egale cu un centimetru, atunci zona sa va fi egală cu:

Să examinăm dreptunghiului prezentat în figura 63. Această casetă este format din trei fâșii, iar fiecare astfel de bandă este împărțit în cinci pătrate egale având o latură de 1 cm.

Să încercăm să găsim zona sa. Deci, ia cinci pătrate, și se înmulțește cu trei dungi și de a obține o suprafață egală cu 15 centimetri pătrați

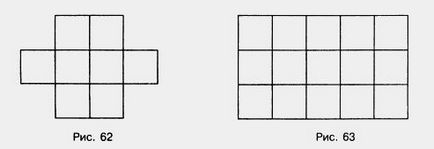
Luați în considerare următorul exemplu. Figura 64 prezintă un dreptunghi ABCD, linia rupt klmn este împărțit în două părți. Prima parte este egală cu suprafața de 12 cm2, și are o a doua suprafață de 9 cm2. Acum, să găsim aria întregului dreptunghi:

Deci, luăm trei și se înmulțește cu șapte, și de a obține 21 cm:

3 • 7 = 21 cmp În acest caz, 21 = 12 + 9.

Și am ajuns la concluzia că întreaga zonă din figura noastră este egală cu suma suprafețelor părților sale individuale.

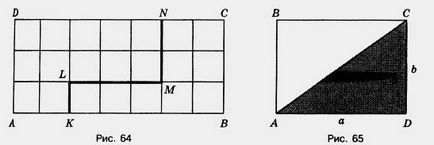
Luați în considerare un alt exemplu. Și astfel în Figura 65 arată un dreptunghi cu ajutorul segmentului de curent alternativ este împărțit în două triunghi egal ABC și ADC

Și astfel, după cum știm deja, că pătrat - aceasta este acelasi dreptunghi, dar are laturile egale, atunci suprafața fiecărui triunghi este egală cu jumătate din suprafața întregului dreptunghiului.

Imaginați-vă că partea de pătrat este egală cu o, atunci:

Am tras concluzia că zona cu formula pătratului va avea următoarea formă:

O a2 înregistrare se numește pătrat a.

Și astfel, în cazul în care partea noastră a pătrat este de patru centimetri, zona sa va fi:

4 • 4, adică 4 * 2 = 16 centimetri pătrați

Întrebări și Sarcini

• Găsiți zona figurii, care este împărțită în șaisprezece pătrate ale căror laturi sunt egale cu un centimetru.
• Gândiți-vă cu formula dreptunghi și scrie-l în jos.
• Care măsurători sunt necesare pentru a face să se cunoască aria unui dreptunghi?
• Definiți cifrele egale.
• Poate avea forme egale zone diferite? Un perimetru?
• Dacă știți zona părților individuale ale figurii, cum știm suprafața totală?
• Formulați și notați ceea ce este egal cu aria pătratului.

informații istorice

Stiati ca oamenii vechi din Babilon au putut calcula aria unui dreptunghi. La fel cum egiptenii antici au făcut calcule de diferite forme, dar formulele exacte ei nu au știut că avea o eroare de calcul mic.

În cartea sa, „Elements“, celebrul matematician grec Euclid, descrie diferite metode de calcul zona de diferite forme geometrice.