Derivatele de ordin superior - exemple de calcul

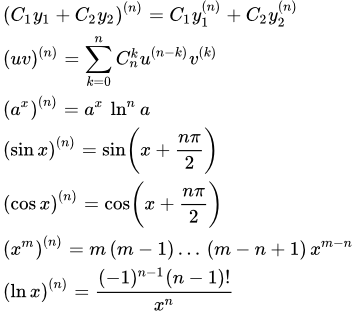
Exemplele de calcul al derivaților de ordin superior funcții explicite. Este util pentru calcularea derivatelor de ordinul n-lea formula.

Aici considerăm cazul în care variabila y depinde de variabila x în mod explicit:






.
Diferențierea funcția variabilei x. pentru a produce ordinul întâi, sau pur și simplu derivatul:
.
Rezultatul este o caracteristică nouă. care este un derivat al unei funcții. Diferențierea această nouă caracteristică a variabilei x. un derivat al doilea ordin:
.
Diferențierea caracteristică. pentru a produce al treilea ordin:
.
Și așa mai departe. Diferențierea originale timpii de funcția n, obținem derivata de ordinul n sau n-lea derivat:
.

Derivații pot fi accidente vasculare cerebrale, notate cu cifre romane, cifre arabe în paranteze sau fracțiune de diferențiale. De exemplu, derivații de a treia și a patra comandă sunt denumite după cum urmează:
;
.

Mai jos sunt formule ce pot fi utile în calculul derivatelor de ordin superior.

derivaților utili cu formula ordine n-lea

Derivata unei sumă de funcții:
.
în cazul în care - constantă.

Formula produsului derivat Leibniz a două funcții:
.
unde
- coeficienții binomiali.

Găsiți derivați din prima și a doua funcții de comandă următoare:
.

Găsim derivata din prima comanda. Vom lua un semn constant al derivatului cu formula și utilizarea derivatelor din tabel:
.
Vom aplica regula de diferențiere o funcție compozit:
.
Aici.
Vom aplica regula pentru diferențierea o funcție compozit și de a folosi punctul de derivați:
.
Aici.

Așa că am găsit derivata din prima ordine:
.
Pentru a găsi derivata de ordinul al doilea, trebuie să găsim derivata derivata din prima comanda, care este funcția:
.






A nu se confunda cu notație, vom nota această literă funcție.
(A1.1).
Apoi, derivata a doua comandă a funcției inițiale este derivata funcției.
.

Găsim derivata funcției. Este mai ușor de făcut utilizând derivatul logaritmică. Logaritm (A1.1):
.
Acum distingem:
(A1.2).
Dar - este o constantă. derivatul său este zero. Derivat din care le-am găsit deja. Ostalnve găsi derivați ai regulii funcției compozit pentru diferențiere.
;
;
.
Înlocuim în (A1.2)

Găsiți derivatul de al treilea ordin:
.

Găsim derivata din prima comanda. Pentru a face acest lucru, vom lua un semn permanent al derivatului, folosind tabelul de derivat și să aplice regula pentru identificarea derivata unei funcții compozit.

Aici.
Așa că am găsit derivata din prima ordine:
.

Am găsit derivata a doua. Pentru a face acest lucru, vom găsi derivata. Aplicarea fracțiuni derivate formula.
.
Derivatul de ordinul al doilea:
.

Acum vom găsi derivații de ordinul trei necesare. A face acest lucru, vom diferenția.
;
;

Derivata de ordinul al treilea este
.

Găsiți derivatul a șasea comandă următoarele funcții:
.

Dacă deschideți paranteze, va fi clar că funcția inițială este un polinom de grad. Am scrie sub forma unui polinom:
.
în cazul în care - coeficienți constanți.

În continuare, se aplică derivatul n-lea formula a funcției de putere:
.
Pentru un derivat al șaselea ordin (n = 6), avem:
.
Acest lucru arată că, atunci când. Când avem:
.

Utilizați formula funcțiilor derivate ale sumei:

Astfel, pentru a găsi derivat al șaselea ordinul a funcției inițiale, avem nevoie de a găsi doar coeficientul polinom de cel mai înalt grad. Găsiți-l prin înmulțirea cele mai mari puteri din produsul suma funcției inițiale:

Găsiți derivatul n-lea a funcției
.

Găsiți derivatul n-lea dintre următoarele funcții:
.
în cazul în care - constantă.

În acest exemplu de calcul care se realizează folosind numere complexe. Să presupunem că avem unele funcții complexe
(A5.1).
în cazul în care - o funcție a variabilei x reale;
- unitatea imaginară.
Diferențierea (A.1) de n ori, avem:
(A5.2).
Uneori este mai ușor de a găsi derivat n-lea a funcției. Apoi derivatul n-lea de x este definit ca părțile reale și imaginare ale derivatului n-lea.
;
.

Vom aplica această metodă pentru a rezolva exemplul nostru. Luați în considerare funcția
.
Aici am aplicat formula lui Euler
.
și a introdus notația
.
Apoi derivatul n-lea a funcției inițiale este dată de:
.

Vom găsi derivat n-lea a funcției
.
La aceasta vom aplica formula:
.
În cazul nostru,
.
atunci
.

Așa că am găsit derivatul n-lea a funcției complexe.
.
în cazul în care.
Haideți să găsim o parte reală a functiei.
Pentru aceasta vom reprezenta un număr complex în formă exponențială:
.
în cazul în care;
;.
atunci
;

Să.
apoi;
.
Când.
.
.
.
Și vom obține derivatul cu formula n-lea al cosinusul:
.