Elementele analizei vectoriale
Analiza vector Zlementy
15.1. câmpuri vectoriale. Diferențial și integral
caracteristicile câmpurilor vectoriale
15.1.1. linii vectoriale. ecuații diferențiale
linii de câmp vectorial
Definiție 1. Un câmp vectorial este o parte a spațiului (sau întregul spațiu), în care fiecare punct M dat orice fenomen fizic, caracterizat printr-o mărime vectorială.
Dacă ar fi introdus în spațiul dreptunghiular cartezian sistem de coordonate, vectorul de referință - funcția de câmp este redusă la trei ordine de funcții scalare:
Cele mai simple caracteristici geometrice câmpuri vectoriale sunt vector și vectorul tub de linie.
Liniile de câmp vectorial 2. Determinarea sunt numite linii (curbe) la fiecare punct M unde direcția tangentei coincide cu direcția câmpului în acest moment.
Definiție 3. Un vector numit suprafață tub format din linii vectoriale care trec prin punctele situate într-un anumit domeniu al unei curbe închise care nu coincid (cel puțin parțial) cu - linie sau vector.
În cazul în care câmpul este dată de (1.1), ecuația liniilor vectoriale este dată de un sistem de ecuații diferențiale
Notă. Metode de rezolvare a sistemelor (1.2) (sisteme în formă simetrică) sunt considerate în teoria ecuațiilor diferențiale.
Definiție 4. Un câmp vectorial este declarat a fi plat, în cazul în special selectat un sistem de coordonate, are forma:
Sistemul de ecuații (1.2) pentru aceste domenii are forma
și astfel liniile vectoriale plat câmp - l curbe situate în planuri paralele cu planul Oxy.
Exemplul 1. Găsiți câmpul vectorial (vector = const; - vectorul raza unui punct).
Decizie. Să; atunci
.
Formăm ecuațiile diferențiale ale sistemului de linii vectoriale (1.2):
.
Acest sistem este o metodă de rezolvare a combinațiilor integrabile. Pentru combinația integrabil se multiplica numărătorul și numitorul primei fracțiuni la x. al doilea - de y. al treilea - pe z; se adaugă termenul de termen. Prin proprietatea proporțiilor obținem
,
din care se obține o combinație integrabile :; integrarea acesteia, vom obține - prima integrală a sistemului. O a doua combinație integrabile obținută prin înmulțirea numărătorul și numitorul fracției pentru primul, al doilea - pe, al treilea - pe; se adaugă termenul de termen, obținem
;
prin urmare, prin urmare.
Astfel, sistemul determină ecuațiile dorite linii vectoriale: centrele de cerc din care sunt pe o linie dreaptă care trece prin originea în direcția vectorului; planul în care se află perpendicular pe linie dreaptă.
Exemplul 2. Găsiți liniile câmpului magnetic vector conductor de curent infinit.
Decizie. Noi credem că conductorul este direcționat de-a lungul axei Oz. și în aceeași direcție curent este curge. Vectorul câmpului magnetic generat de curentul, este în cazul în care - vectorul curent, - vectorul raza unui punct; - distanța de la axa conductorului înainte de punctul M. Avem, în continuare, ecuația (1.2 ¢) ia forma :, unde - cu vectorul linii sunt cercuri centre pe axa Oz.
15.1.2. Vectorul câmp de curgere
1. Determinarea fluxului câmp vectorial
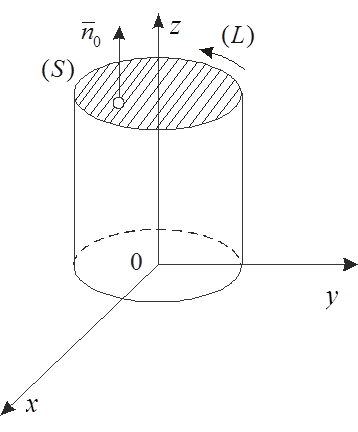
Să considerăm câmpul vectorial, în care proeminențele - funcții continue în unele regiuni (V). Să considerăm un (netedă pe porțiuni) suprafață netedă bilaterală orientată (S) (adică, cu suprafața selectată cu două fețe pe aceasta direcție normală).
Definiția. câmp II vector Stream prin suprafață orientată bidirecțională (S) se numește suprafață integrală a primului tip de pe suprafața (S):
Aici, - un vector unitate normală lateral (S) selectat; ds - aria suprafeței elementului (S).
Notă. În cazul unei suprafețe închise este orientat dirijat în interiorul regiunii normale (V) la exterior. Partea cu direcția pozitivă a normalului este numită partea pozitivă a suprafeței.
Pentru debitul poate da următoarea intrare prin integralelor de suprafață ale primului și al doilea tip:
în cazul în care - adică - zona de proiecție pe planul Oyz. Oxz. Oxy respectiv.