Numere complexe și operații asupra acestora - studopediya

Numere complexe și operații asupra acestora

Chiar și cele mai simple operații algebrice cu numere reale (rădăcina pătrată a unui număr negativ, soluția ecuației pătratice cu discriminant negativ) este de ieșire în afara setului de numere reale. O altă generalizare a conceptului de număr conduce la numere complexe. O caracteristică remarcabilă a setului de numere complexe este că acesta este închis în raport cu operațiile matematice de bază. Cu alte cuvinte, operațiile matematice de bază asupra numerelor complexe nu sunt eliminate din setul de numere complexe.

număr complex (în formă algebrică) este o expresie

în cazul în care - număr real arbitrar - unitate imaginară. determinată de condiția.

Numărul se numește partea reală a unui număr complex este desemnat (de la „realis“ limba latină), numărul se numește partea imaginară a unui număr complex și este notat cu (din latinescul „imaginarius“).

Și două numere complexe sunt egale dacă și numai dacă acestea sunt părțile reale și imaginare :. . Două numere complexe sunt egale sau nu este egal (conceptul de „mai mult“ și „mai puțin“ nu sunt introduse pentru numere complexe).

Complex-conjugat al numărului este numărul. Aparent, numărul de complex conjugat la numărul coincide cu numărul. .

operații aritmetice. Adunare, scădere și înmulțirea numerelor complexe produse de regulile obișnuite de algebră.

Exemplul 1 definește un număr complex. .

Problema 1. Fie și - o pereche de numere complexe conjugate. Arătați că suma lor este un număr real, diferența - un număr imaginar, iar produsul are un număr non-negativ validă.

Notă. Numărul de grad poate fi reprezentat ca un tabel

Interpretarea geometrică a unui număr complex.

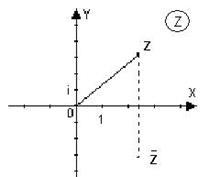
Luați în considerare carteziene sistemul de coordonate. Este reprezentată grafic de-a lungul axei abscisa a unui număr complex. iar axa verticală - partea imaginară. Obținem un punct cu coordonate. Astfel, fiecare număr complex corespunde la un punct al planului. Pe de altă parte, fiecare punct al planului poate fi asociat cu un număr complex. partea reală este egală cu abscisa punctului, iar partea imaginară este egală cu ordonata punctului. Astfel, între planul numerelor complexe și puncte la o corespondență. (Anterior, vorbeam despre o corespondență unu-la-unu între numerele reale și punctele liniei numărul).

Avionul, care reprezintă puncte numerele complexe se numește un plan complex. Pentru a-l distinge de planul real, în colțul din dreapta sus al scrisorii scrise. încercuite. Axa abscisa în acest plan se numește axa reală și axa ordonatei - axa imaginară. Complex-conjugat - o imagine în oglindă a unui număr predeterminat în raport cu axa reală. Originea numit punctul nul. Distanța numărului complex de origine numit modulul acelui număr:

.

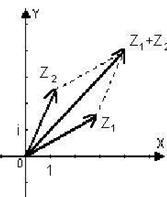
Modulus a diferenței dintre două numere complexe - este distanța dintre punctele corespunzătoare:

Fiecare punct din planul complex asociază vectorul cu originea la punctul zero, iar la sfârșitul anului, la acel moment. Evident, această corespondență este unu-la-unu. În această interpretare a părților reale și imaginare ale unui număr complex - prima și a doua componente vectoriale. Suma acum pare o diagonală a paralelogramului construit pe vectorii și. înțeleasă ca diferență. număr complex Modulul reprezintă o lungime a vectorului. Geometric evident este inegalitatea triunghiului în planul complex :.

Exemplul 7. Identificați locul geometric al punctelor pe planul complex, pentru care

Decizie. a) As. având în vedere dubla inegalitatea poate fi rescrisă ca :. Am primit benzi verticale.

b) Din moment. având în vedere dubla inegalitatea poate fi rescrisă ca :. Am primit bandă orizontală. Sarcini c) și d) să decidă pe cont propriu.

Exemplul 8. Se indică locul geometric al punctelor pe planul complex, pentru care a); b); c).

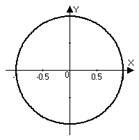
Decizie. a) Modulul unui număr complex - aceasta este lungimea vectorului care vine de la punctul zero la un punct. și anume distanța de la origine la punctul. Prin urmare, în cazul în care acesta este un plan de locus de puncte echidistante de origine - este un cerc (în acest caz, raza cercului este 1). Puteți traduce problema în limba cartezian coordonate:

b) Este vorba despre locul geometric al punctelor care se află în afara cercului de rază (centrată la origine).

c) punctele sunt în ring, și între cercurile de rază.

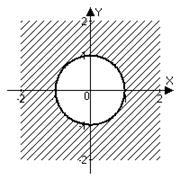
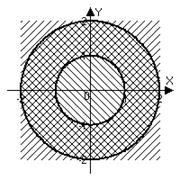
Exemplul 9. Dă locus pe planul complex, pentru care a); b); c).

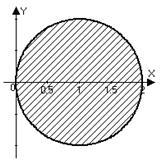
Decizie. a) modulul diferența - este distanța dintre un punct și un punct din planul complex 1. Prin urmare, este un locus de puncte echidistante (la distanță 1) de la punctele 1, - un cerc cu raza de 1 cu centrul în punctul (1, 0). În limba de origine:

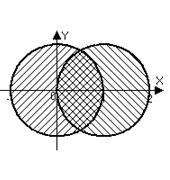
b) Punctele sunt simultan într-un cerc cu centrul său la originea și în cercul cu centrul deplasat la punct. .

c) Este punctul de dreapta semiplanul. situată în interiorul cercului. .

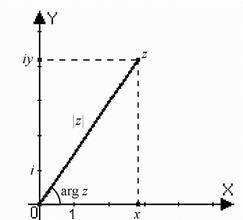
forma trigonometrică a unui număr complex. Argumentul unui număr complex numit unghi. care este un vector cu direcția pozitivă a axei reale. Acest unghi este determinat în mod unic:

În cazul în care - valoarea principală a argumentului, acesta este eliberat de inegalitățile (adică, planul complex este tăiat pe axa reală la stânga de origine).

Prima coloană este specificată pentru numărul. situată pe axa reală sau imaginară, iar coloana a doua - pentru restul numerelor complexe.

Notăm. Din moment. . este un număr complex poate fi reprezentat în formă trigonometric:

Și două numere complexe. definit în forma trigonometric

din cauza ambiguitatea argumentului sunt egale dacă și numai dacă. .

Exemplul 10. Găsiți modulii și argumentele, precum și valorile principale ale argumentelor de numere complexe. Înregistrați fiecare dintre ele în formă trigonometrice.

Decizie. Modulele acestor numere sunt aceleași:

Fiecare număr este argumentul, având în vedere trimestru, care este punctul corespunzător.

1) punctul se află în primul cadran, apoi

Forma trigonometrică. Este luată în considerare - frecvența sinus și cosinus.

2) punctul se află în al doilea cvadrantul, mijloace

3) se află punctul în al treilea cadranului, aceasta înseamnă

4) Punctul se află în al patrulea trimestru, apoi,

Înmulțirea și împărțirea numerelor complexe în formă trigonometrice. Să numerele și sunt definite în formă trigonometric :. . Înmulțiți-le:

Amintindu-și formula pentru cosinusul și sinusul suma a două unghiuri, obținem

Vedem că în înmulțirea numerelor complexe înmulțit modulele lor și sunt adăugate argumente. Semnificația geometrică a acestei operațiuni: și numerele care reprezintă vectorii în planul complex, care provin de la punctul zero, vom vedea că vectorul obținut din vectorul „întindere“ în timp și de a porni un colț.

Pentru a obține formula privată:

Exemplul 11. Găsiți produsul și coeficientul de numere

Decizie. În conformitate cu formula (1) se poate scrie:

Verificăm rezultatul prin înmulțirea acestor numere în formă algebrică:

În conformitate cu formula (2) găsim

această operațiune este în formă algebrică poate fi scris ca:

Construirea unui număr complex la o putere. De la formula (1), că exponentiation unui număr complex se realizează conform regulii

Exemplul 12. Se calculează 1); 2).

Decizie. 1) Am primit înregistrarea unui număr complex în formă trigonometric :. Conform formulei (3) este situat. Același rezultat a fost obținut în exemplul 4c de mai sus) folosind binomial lui Newton.

2) În primul rând, imaginați-vă numerele în formă trigonometrice.

Acesta se află în al patrulea trimestru, atunci. prin urmare

Rămâne să utilizeze formula (3):

Dezvăluind cubul a diferenței, vom obține același rezultat (verificați!).

In formula (3) este transformata in formula DeMoivre:

Cu este ușor de a obține relația care exprimă sinus și cosinus de unghiuri multiple și.

Exemplul 13. Pentru a exprima și prin și.

Decizie. Punerea în formula DeMoivre. obținem:

De la stânga pentru a dezvălui valoarea cubului și să colecteze alți termeni asemănători:

Aici avem asta. Am ajuns la egalitatea a două numere complexe în formă algebrică

ceea ce este adevărat dacă și numai dacă, atunci când sunt părțile reale și imaginare ale acestor numere.

Ecuația dă părțile reale;

echivalând piese imaginare, obținem.

Eliminarea rădăcina numărului complex. Dacă numerele complexe și sunt legate. atunci. Reprezentarea numerelor în formă trigonometrice:

Presupunem că există - valoarea principală a unui argument.

Sarcina noastră - cu privire la numărul specificat (de exemplu, cunoscute și) pentru a defini (de exemplu, ambele). În conformitate cu formula (3) poate fi scrisă ca ecuația

Din egalitatea a două numere complexe în formă trigonometric urmează:

Aici - rădăcina de gradul mii de număr real non-negativ. Prin urmare, pentru rădăcina de număr complex lea grad obținem formula

Presupunând secvențial. Obținem valori diferite:

Toate aceste rădăcini au aceleași module. și anume punctele corespunzătoare sunt situate pe raza unui cerc centrat în origine. Argumentele două rădăcini adiacente de pe unghi diferit. Prin urmare, toate valorile gradului de rădăcină -lea numere complexe sunt în nodurile -gon corecte înscrise într-un cerc de rază.

Exemplul 14. Gaseste toate valorile gradului rădăcină-lea a numărului complex și le reprezintă în planul complex, dacă

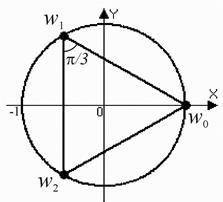
Decizie. 1) În primul rând, vom găsi modulul și argumentul unui număr complex. . Ecuația (5) ia forma

Punctele sunt la vârfurile unui triunghi echilateral înscris într-un cerc de rază, o rădăcină - este un număr real. Argumentele doi pixeli adiacenți diferă cu un anumit unghi. Rețineți că.

2) Aici. . prin urmare

,

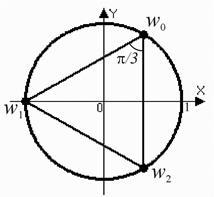
Punctele sunt la vârfurile unui triunghi echilateral înscris într-un cerc. rădăcină este un număr real. Rețineți că. Comparați cu pr.12.2 rezultate în cazul în care au primit. și anume .

3) Aici. și

,

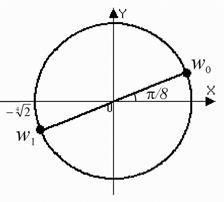
4) Aici și

. care conduce la două numere:

Problema 3. Efectuați pr.14 de locuri de muncă în cazul în care 1). 2).

Exemplul 15. Aranjarea factori liniari trinom pătrat

Decizie. 1) Să considerăm ecuația pătratică. discriminant sale. Deci, fără rădăcini reale. De la pr.14.4 asta. Conform formulei pentru rădăcinile unei ecuații pătratice. Am primit două rădăcini complexe conjugate și. În conformitate cu rădăcinile găsite putem extinde trinomul pătratic în factori liniari:

2) Să considerăm ecuația pătratică. discriminant sale. rădăcini reale. De la pr.14.4 asta. Conform formulei pentru rădăcinile unei ecuații pătratice. Am primit două rădăcini complexe conjugate și. În conformitate cu rădăcinile găsite ale trinom pătratic descompunem în factori liniari:

Vă rugăm să rețineți că o ecuație pătratică cu coeficienți reali are o pereche de rădăcini complexe conjugate.

Sarcina 4. Verificați dacă următoarea descompunere în factori liniari

Forma exponențială a unui număr complex. Formula lui Euler (sa fie dovedit mai târziu):

Acesta vă permite să înregistrați un număr complex în formă exponențială:

Deoarece formula lui Euler și - frecvența sinus și cosinus urmează:

Exemplul 16. Numerele scrise în formă exponențială.

Este ușor de verificat validitatea:

Comparați acest raport cu regulile de multiplicare și împărțirea exponentiation numerelor complexe în formă trigonometrice.

Exemplul 17: compara și numere complexe.

Decizie. De la pr.16 :. Există numere și module. Evidențierea în indicele numărului de termeni, ori. reprezentată în formă. ca multiplicator. Înseamnă.