Scadere de fracțiuni cu diferite numitori

Cum fracțiuni ale căror numitori sunt aceleași scădere

Shot - este același număr, care poate produce o varietate de acțiuni. Ele se deosebesc de numere întregi este prezența numitorului. De aceea, atunci când efectuează operațiuni cu fracții nevoie pentru a explora unele dintre caracteristicile și regulile. Cel mai simplu caz este o scădere a fracțiunilor a căror numitori sunt reprezentate ca același număr. Efectuați această acțiune nu va fi dificil, dacă știi regula simpla:

• Pentru a deduce o fracțiune de o secundă, este necesar din numărătorul fracției fără scăderea scade numărătorul fracției deductibile. Acest număr record de diferențe în numărătorul și numitorul aceluiași subiect: k / m - b / m = (k-b) / m.

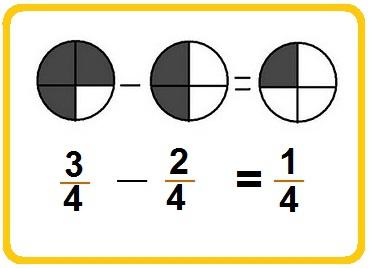
Exemple scăzând fracțiuni ale căror numitori sunt aceleași

Să vedem cum arată pe exemplu:

7/19 - 3/19 = (7 - 3) / 19 = 4/19.

Fără scăderea numărătorul fracției „7“ scade numărătorul fracției deductibile „3“, pentru a primi „4“. Acest număr vom scrie în numărătorul răspuns, și a pus la numitor același număr care a fost în numitorul prima și a doua fracțiuni - „19“.

Imaginea de mai jos prezintă câteva exemple.

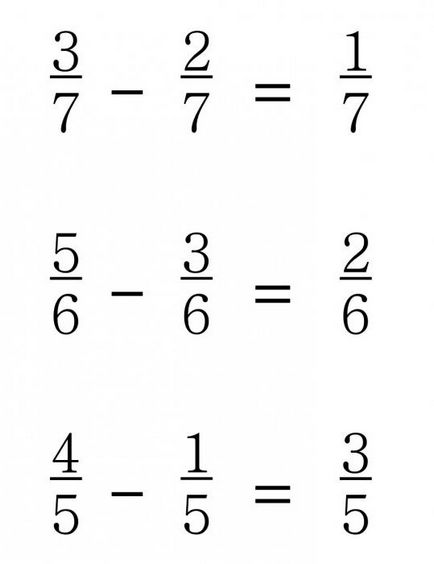
Să considerăm un exemplu mai complex, care a produs scăderea fracțiilor cu același numitor:

29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29-3 - 8-2 - 7) / 47 = 9/47.

Fără scăderea numărătorul fracției „29“, scăzând numărătorii la rândul său, toate fracțiile ulterioare - „3“, „8“, „2“, „7“. Ca rezultat, vom obține rezultatul „9“, care este scris în numărătorul răspunsul, și scrie în numitorul este numărul care este în numitorul tuturor acestor fracțiuni - „47“.

Adăugarea de fracții cu același numitor

Adunarea și scăderea fracțiilor se realizează pe același principiu.

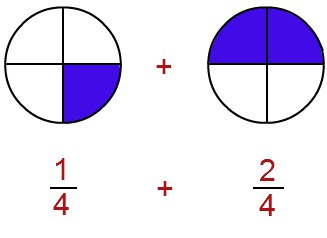
• Pentru a plia fracțiuni ale căror numitori sunt aceleași, trebuie să adăugați până numărătorii. Numărul primit - suma numărătorul și numitorul va rămâne același: k / m + b / m = (k + b) / m.

Să vedem cum arată pe exemplu:

Pentru numărătorul primul termen al fracțiunii - „1“ - adăugarea numărătorul al doilea termen al fracțiunii - „2“. Rezultatul - „3“ - scrie în suma numărătorul și numitorul părăsi este aceeași ca și cea prezentă în fracțiunile - „4“.

Fracțiunile cu diferite numitorilor și scăderea

Acțiunea cu fracții care au același numitor, am discutat deja. După cum puteți vedea, știind reguli simple pentru a rezolva aceste exemple destul de ușor. Dar ce se întâmplă dacă aveți nevoie pentru a efectua o acțiune cu fracții care au diferite numitori? Mulți elevi de gimnaziu vin la dificultatea unor astfel de exemple. Dar aici, de asemenea, dacă cunoașteți principiul soluțiilor, exemple nu vor mai fi prezenți pentru tine dificultate. Și aici există o regulă, fără de care soluția acestor fracțiuni este pur și simplu imposibil.

Pentru a face o scădere de fracțiuni cu diferite numitori, trebuie să le aducă la același mai mic numitor comun.

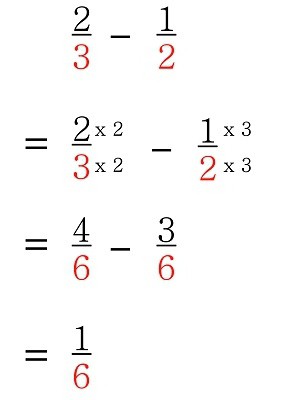
Pentru a afla cum se face asta, vom vorbi mai mult.

proprietate fracțiuni

Pentru mai multe fracțiuni conduc la același numitor, pentru a fi utilizat în rezolvarea cea mai importantă proprietate a fracțiunilor: după împărțirea sau înmulțirea numărătorul și numitorul cu același număr se va rostogoli egal cu aceasta.

De exemplu, fracția 2/3 poate avea numărătorii, cum ar fi „6“, „9“, „12“, și așa mai departe. G. se poate lua de exemplu, forma oricărui număr care este un multiplu de „3“. După numărătorul și numitorul, înmulțim cu „2“, veți obține fracția 4/6. După numărătorul și numitorul fracției vom multiplica sursa la „3“, vom obține 6/9, și în cazul în care un efect similar pentru a produce cu numărul „4“, obținem 8/12. acesta poate fi scris ca o singură ecuație după cum urmează:

2/3 = 4/6 = 6/9 = 8/12 ...

Cum de a cita câteva fracțiuni la același numitor

Luați în considerare modul de a aduce mai multe fracțiuni la același numitor. De exemplu, să ia fracțiunile prezentate în figura de mai jos. În primul rând avem nevoie pentru a determina cât de multe poate fi un numitor pentru toate acestea. Pentru a facilita extinderea numitori existente de factoring.

Numitorul fracției 1/2 și 2/3 nu pot fi descompuse în factori. 7/9 Numitorul are două factor 7/9 = 7 / (3 x 3), numitorul fracției 5/6 = 5 / (2 x 3). Acum aveți nevoie pentru a determina ce va fi cea mai mică dintre toate cele patru fracțiuni factori. Deoarece prima fracțiune la numitor are numărul „2“, atunci trebuie să fie prezentă în toate numitorilor din fracția 7/9 are două triplete, atunci ele trebuie de asemenea să fie prezente la numitor ambele. Având în vedere cele de mai sus, determinăm că numitorul este format din trei factori: 3, 2 și 3 este de 3 x 2 x 3 = 18.

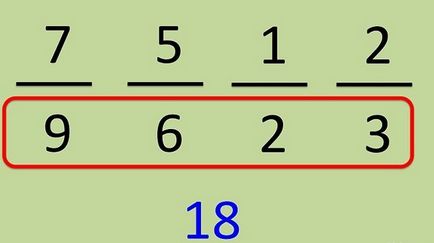
Luați în considerare prima fotografie - 1/2. În numitorul său are „2“, dar nu există o singură cifră „3“, și trebuie să existe două. Pentru a face acest lucru, se înmulțește cu numitorul celor două triplete, dar, în funcție de proprietatea fracțiunii, numărătorul și trebuie să ne înmulțim cu două camere triple:
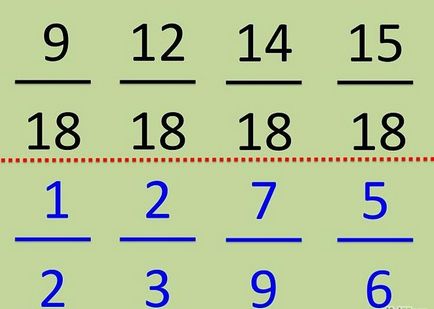
= 1/2 (1 x 3 x 3) / (2 x 3 x 3) = 9/18.

produc în mod similar cu acțiune fracțiunile rămase.

• 2/3 - la numitor este lipsește unul din trei și una din două:
  = 2/3 (2 x 3 x 2) / (3 x 3 x 2) = 12/18.
• 7/9 sau 7 / (3 x 3) - la numitor lipseste cate doua:
  7/9 = (7 x 2) / (9 x 2) = 14/18.
• 5/6 sau 5 / (2 x 3) - la numitor lipseste triplete:
  5/6 = (5 x 3) / (6 x 3) = 15/18.

Toate în toate se pare ca acest lucru:

Cum se scade și se adaugă în sus fracțiuni cu diferite numitori

După cum sa menționat mai sus, în scopul de a efectua adunarea sau scăderea de fracțiuni cu diferite numitori, acestea ar trebui să conducă la un numitor comun, și apoi să profite de regulile de scăderea fracțiilor cu același numitor, care a fost deja spus.

Uită-te la un exemplu: 4/18 - 3/15.

Găsim multiplu de 18 și 15:

• Numărul 18 este compus din 3 x 2 x 3.
• Numărul 15 este format dintr-un 5 x 3.
• Pliul generală va consta din următorii factori de 5 x 3 x 3 x 2 = 90.

Când este găsit numitor, este necesar să se calculeze multiplicatorul, care va fi diferit pentru fiecare fracție, care este numărul care va fi necesar să se multiplice nu numai numitorul, dar numărătorul. Pentru acest număr vom găsi (mai multe comune), împărțit la numitorul fracției, ceea ce este necesar pentru identificarea factorilor suplimentari.

• 90 împărțit la 15. Numărul rezultat „6“ este un factor la 3/15.
• 90 împărțit la 18. Numărul rezultat „5“ este un factor la 4/18.

Următoarea etapă a soluțiilor noastre - aducerea fiecare fracție la numitor „90“.

Cum se face acest lucru, am vorbit deja. Să considerăm, așa cum scrie în Exemplu:

(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.

În cazul în care fracțiunea cu număr mic, este posibil să se determine numitorul comun ca în exemplul prezentat în imaginea de mai jos.

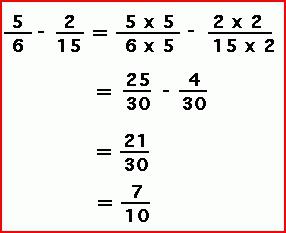
a produs în mod similar și adăugarea de fracții având diferite numitori.

Adunare și scădere a fracțiilor cu părți întregi

Scadere de fracțiuni și adăugarea lor, am discutat deja în detaliu. Dar cum să faci o scădere, în cazul în care există o fracțiune din întreg? Din nou, utilizați câteva reguli:

• Toate fracțiunile cu o parte întreagă, tradus greșit. În cuvinte simple, scoateți partea întreagă. Pentru aceasta, porțiunea număr întreg este înmulțit cu numitorul fracției obținute prin adăugarea produsului la numărătorul. Acel număr, care se obține în urma acestor acțiuni - numărătorul fracții improprii. Numitorul rămâne neschimbat.
• În cazul în care fracțiunile au diferite numitori, ar trebui să le aducă la fel.
• Efectuați adăugarea sau scăderea a acelorași numitori.
• La primirea fracțiunilor necorespunzătoare să aloce o parte a întregului.

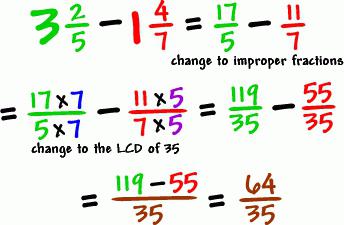
Există o altă cale prin care se poate efectua adunarea și scăderea fracțiilor cu părți întregi. În acest scop, acțiunile sunt efectuate separat de întregi părți, și operațiuni separate cu fracții, iar rezultatele sunt înregistrate împreună.

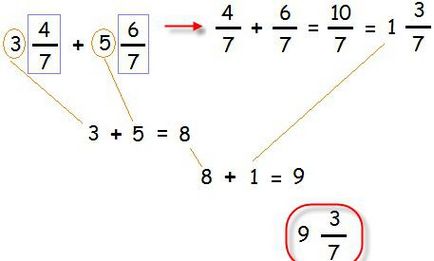
Exemplul de mai sus este compus din fracțiuni care au același numitor. În cazul în care numitorilor sunt diferite, ele trebuie să conducă la fel, și pentru a efectua acțiuni suplimentare, așa cum se arată în exemplul.

Scadere de fracțiuni de un întreg

Un alt dintre soiurile de operațiuni cu fracții este cazul atunci când trebuie să ia o fracțiune de un număr natural. La prima vedere se pare ca un exemplu de dificil de rezolvat. Cu toate acestea, este destul de simplu aici. Pentru a rezolva aceasta trebuie tradus într-o fracție întreagă cu numitorul fiind că se scade în fracțiuni. scădere produc în plus, scădere analoagă cu aceleași numitori. De exemplu, se pare ca acest lucru:

7 - 4/9 = (7 x 9) / 9 - 4/9 = 53/9 - 4/9 = 49/9.

Având în vedere în acest articol scăderea fracțiilor (gradul 6) este baza pentru soluția de mai multe exemple complexe, care sunt discutate în următoarele clase. Cunoașterea acestui subiect sunt folosite mai târziu pentru a rezolva funcții, derivate și așa mai departe. De aceea este foarte important să se înțeleagă și să înțeleagă operațiunile cu fracții, discutate mai sus.