Cum de a găsi aria figurii

Știe și să poată să calculeze aria de diferite forme au nevoie pentru a rezolva probleme geometrice simple nu numai. Nu se poate face fără aceste cunoștințe și în pregătirea sau revizuirea estimărilor pentru repararea spațiilor, pentru calcularea numărului de consumabile necesare. Deci, să ne uităm la modul de a găsi zona de diferite forme.

O parte a planului închisă de buclă închisă se numește o zonă a planului. Numărul suprafeței exprimate în unități închise pătrate în aceasta.

Pentru a calcula aria formelor geometrice de bază, este necesar să se utilizeze formula corectă.

zonă a unui triunghi

legendă:

• S - zona dorită,
• a, b, c - lungimea laturilor unui triunghi,
• h - înălțimea triunghiului dorit
• γ - Colț situată între o parte și partea b,
• r - raza cercului (înscris într-un triunghi)
• 
  R - raza unui cerc (circumscris în jurul triunghiului)
• p - jumătate din perimetrul triunghiului.

1. Dacă se cunoaște h, o, zona dorită a triunghiului este definit ca produsul dintre lungimile laturilor triunghiului și înălțimea este coborâtă spre această latură, împărțit în jumătate: S = (a-h) / 2
2. Dacă știm, b, c, atunci suprafața dorită este calculată prin formula lui Heron: rădăcina pătrată luată de produs obținut jumătate din perimetrul triunghiului și cele trei diferențe jumătate din circumferința și fiecare latură a triunghiului: S = √ (p · (p - a) · (p - b) · (p - c)).
3. Dacă știm a, b, γ, aria triunghiului este definit ca produsul a două jumătăți de laturi, înmulțită cu sinusul unghiului dintre aceste laturi: S = (a · b · păcatul γ) / 2
4. Dacă știm a, b, c, R, suprafața necesară este definită ca produsul dintre lungimile tuturor diviziunea laturi ale triunghiului în patru raza cercului circumscris: S = (a · b · c) / 4R
5. Dacă știm p, r, zona potrivit triunghiului definit prin înmulțirea jumătate a perimetrului pe raza cercului inscris acolo: S = p · r

Zona pătratului

legendă:

• S - zona dorită,
  
• o - lungime laterală,
• d - lungimea diagonalei.

1. Dacă partea este cunoscută, atunci această zonă a figurii este definită ca patratul lungimii laturilor: S = a2
2. Dacă cunoscut d, suprafața pătrată este definită ca jumătate din pătratul lungimii sale diagonale: S = d 2/2

Suprafața unui dreptunghi

legendă:

• S - zona definită,
• a, b - lungimea laturilor dreptunghiului.

1. Dacă știm a, b, atunci aria dreptunghiului definit de produsul dintre lungimile cele două laturi ale sale: S = a · b
2. În cazul în care lungimile laturilor sunt necunoscute, aria dreptunghiului trebuie să fie împărțit în triunghiuri. În acest caz, aria dreptunghiului este definită ca suma suprafețelor de triunghiuri sale constitutive.

Suprafața unui paralelogram

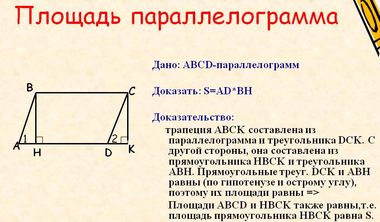
legendă:

• S - zona dorită,
• a, b - lungimea laturilor,
• h - înălțimea de lungimea paralelogramului,
• d1, d2 - lungimea celor două diagonale,
• α - unghiul, situat între laturile,
• γ - Colț situat între diagonalele.

1. Dacă cunoaștem o, h, zona dorită este determinată prin înmulțirea lungimile laturilor și înălțimea este coborâtă la această latură: S = a · h
2. Dacă știm a, b, α, suprafața este determinată prin înmulțirea lungimile laterale paralelogram ale paralelogramului și sinusul unghiului dintre aceste laturi: S = a · b · sin α
3. Dacă știi d1. d2. γ aria paralelogramului este definită ca jumătate din produsul lungimilor diagonalelor și sinusul unghiului dintre diagonalele: S = (d1 · d2 · sinγ) / 2

Zona de romb

legendă:

• S - zona dorită,
• o - lungime laterală,
• h - înălțimea de lungime,
• α - unghi mai mic între cele două părți,
• d1, d2 - lungimea celor două diagonale.

1. Dacă știm o, h, lungimea romburi este determinată prin înmulțirea suprafeței pe lungime înălțimea laturilor care este omis în acest aspect: S = a · h
2. Dacă știm a, α, suprafața rombul determinată prin înmulțirea cu o lungime laterală pătrată și sinusul unghiului dintre laturile: S = a 2 · sin α
3. Dacă știți D1 și D2. atunci suprafața dorită este definită ca jumătate din produsul lungimilor diagonalelor rombului: S = (d1 · d2) / 2

Zona de trapez

legendă:

• S - zona dorită,
  
• a, b - lungimea de 2 baze trapez
• c, d - lungimea laturilor stânga și dreapta ale trapezului,
• h - înălțimea trapezului,

1. Dacă știm a, b, c, d, zona dorită este definită prin formula: S = (a + b) / 2 * √ [c 2 - (((ba) 2 + c 2 -d 2) / (2 (ba )) 2].
2. Cu cunoscut a, b, h, zona dorită este definită ca produsul de jumătate din totalul bazelor și înălțimea trapezului: S = (a + b) / 2 · h

Zona patrulaterului convex

legendă:

• S - zona dorită,
• d1. d2 - lungimea diagonalelor patrulaterului,
• α - unghiul dintre diagonalele,
• p = (a + b + c + d) / 2 - jumătate din perimetrul unui patrulater convex,
• a și b, c și d - lungimea fiecărei laturi a unui patrulater convex,
  
• θ = (α + β) / 2 - jumătate din suma a două colțuri opuse ale unui patrulater convex,
• r - raza unui cerc înscris într-un patrulater convex.

1. Dacă știi d1. d2. α, aria patrulater convex este definită ca jumătate din produsul diagonalelor patrulaterului, înmulțit cu valoarea sinusul unghiului dintre diagonalele: S = (d1 · d2 · păcat α) / 2
2. Cu cunoscut p, r zona patrulater convex definită ca produsul din jumătatea perimetrului patrulaterul de raza unui cerc înscris în patrulaterul: S = p · r
3. Dacă știm a, b, c, d, θ, aria patrulater convex este definită ca rădăcina pătrată a semiperimetrul produselor diferență și lungimea fiecărei laturi a produsului net al lungimilor tuturor laturile și pătratul cosinusul jumătate din suma a două colțuri opuse: S 2 = (p - un ) (p - b) (p - c) (p - d) - abcd · cos 2 ((α + β) / 2)

Zona de cerc

legendă:

• S - zona dorită,
  
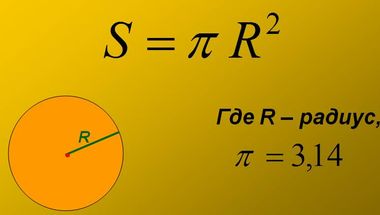
• r - lungimea razei,
• d - diametrul de lungime.

Dacă se cunoaște r, suprafața necesară este definită ca produsul dintre raza numarul π pătrat: S = π r 2

Dacă cunoscut d, aria unui cerc definit ca produs al tt număr pe diametrul la pătrat împărțit la patru: S = (π · d 2) / 4

Suprafața unei figuri complexe

Complexul poate fi împărțit în forme geometrice simple. Suprafața unei figuri complexe este definită ca aria sumă sau componente diferență. Să considerăm, de exemplu, un inel.

denumire:

• S - inel pătrat,
• R, r - razele circumferința interioară și exterioară, respectiv,
• D, d - diametrul circumferinței exterioare și, respectiv, interior.

Pentru a găsi zona inelului, este necesar din zona mai mare cerc ia zona

cerc mai mic. S = S1-S2 = πR 2 -πr 2 = π (R2-2).

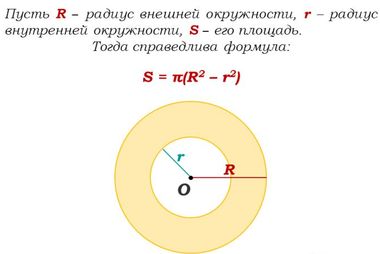
Astfel, dacă știm R și r, aria inelului definită ca diferența dintre pătrate de razele circumferințele exterioare și interioare, înmulțit cu pi: S = π (R2-2).

Dacă se cunoaște D și d, aria inelului este definit ca un sfert din diferența de pătrate de diametre de circumferințele exterioare și interioare, înmulțit cu pi: S = (1/4) (D 2 -d 2) π.

Zona figura umbrită

Să presupunem că într-un pătrat (A) este celălalt (B), (mai mici), și trebuie să găsim o cavitate umplută între cifrele „A“ și „B“. Pune-l în acest fel, „cadru“ de un pătrat mic. Pentru a face acest lucru:

1. Găsim zona unei figuri „A“ (calculat prin formula găsirea unei zone pătrat).
2. În mod similar, vom găsi „B“ zona a figurii.
3. Scădem din zona „A“ zonă „B“. Și astfel ajungem zona figura umbrită.

Acum, că știi cum să găsească zona de diferite forme.