Zona dreptunghiului - formulelor, un exemplu de calcul, calculator
Dreptunghi - un paralelogram în care toate unghiurile sunt de 90 °, iar laturile opuse sunt paralele și egale.
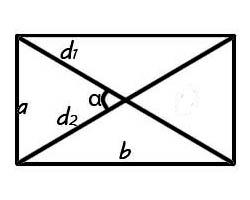
În dreptunghiul există câteva caracteristici convingătoare, care sunt utilizate în rezolvarea o varietate de sarcini, în zona formulei unui dreptunghi și perimetrul acesteia. Iată-le:
- laturi ale dreptunghiului sunt înălțimi sale;
- Lungimile diagonalelor sunt egale între ele;
- Punctul de intersecție a diagonalelor le împărți în jumătate;
Lungimea laturii necunoscute sau diagonala dreptunghiului calculat prin pătrat formula sau triunghi dreptunghiular cu teorema lui Pitagora. Suprafața unui dreptunghi poate fi găsit în două moduri - pe produsul din laturile sale sau prin aria formula unui dreptunghi peste diagonală. Prima și cea mai simplă formulă arată astfel:
Exemplu de calcul suprafață dreptunghi prin această formulă este foarte simplu. Cunoscând cele două părți, de exemplu, a = 3 cm, b = 5 cm, putem calcula cu ușurință aria unui dreptunghi:
Considerăm că zona este egală cu 15 kV într-un dreptunghi. cm.
Zona dreptunghiului pe diagonala
Uneori doriți să aplicați formula pentru aria unui dreptunghi peste diagonală. Pentru aceasta este necesară nu numai pentru a afla lungimea diagonalelor, dar, de asemenea, unghiul dintre ele:
Să considerăm exemplul calculării suprafeței unui dreptunghi peste diagonală. Lăsați un dreptunghi cu o diagonală d = 6 cm, iar unghiul = 30 °. Substitut datele în formula deja cunoscută:
Deci, un exemplu de calcul al zonei unui dreptunghi peste diagonală ne găsim că zona așa că, dacă setați unghiul, este destul de simplu afișate.
Luați în considerare o altă activitate interesantă, care ne va ajuta un pic întindere creierele lor.
Obiectiv: pătrat Dan. Suprafața sa este de 36 mp. cm. Găsiți un dreptunghi perimetru în care lungimea unei laturi este de 9 cm, iar zona este aceeași cu cea dată mai sus pătrat.
Deci, avem câteva condiții. Pentru claritate, noi le scrie pentru a vedea toate parametrii necunoscuți cunoscute și:
Partea din figură sunt paralele și egale. Prin urmare, perimetrul figurii este egală cu dublul sumei dintre lungimile laturilor:
Din zona dreptunghi formulă care este egală cu produsul dintre cele două părți ale figurii, putem găsi lungimea laturii b
De aici:
Substituind datele cunoscute și pentru a găsi lungimea laturii b.
Ne așteptăm ca perimetrul figurii:
Și astfel, știind unele formule simple, putem calcula perimetrul unui dreptunghi, cunoscând zona sa.
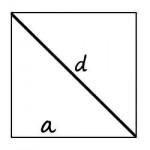
- Zona pătratului
- inel pătrat
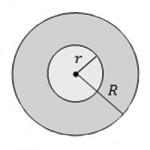
- Zona unui sector de cerc
- Suprafața unui triunghi pe trei laturi
- Zona piramidei hexagonale