Cum de a găsi determinantul matricei

Este cunoscut faptul că determinantul matricei de ordinul al doilea se calculează după cum urmează: din produsele de elemente ale principalelor elemente diagonale ale produsului scade din secundar diagonalei. Prin urmare, este convenabil să se descompună matricea minorilor de ordinul al doilea, și apoi se calculează determinanții acestor minori, precum determinantul matricei originale.






Figura prezintă formula de calcul determinantul orice matrice. Folosindu-l, vom extinde matricea prima pentru minori de ordinul al treilea, iar apoi fiecare minor primit pe minori de ordinul al doilea, ceea ce îl face ușor pentru a calcula determinantul matricei.

Descompunem dimensiunea matricei inițiale formula matricei pentru încă 3 3. matrice suplimentară sau minorii sunt formate din matricea originală prin ștergerea un rând și o coloană. Numărul acestor polinoame minori sunt multiplicate cu elementul de matrice la care se adaugă, semnul determinat de gradul polinomului -1, care reprezintă suma indicilor elementelor.

Acum, fiecare dintre matricele treilea ordin se descompun în același mod pe matricea de ordinul doi. Găsim determinantul unei matrice, și fiecare a obține o serie de polinoame ale elementelor matricei originale, apoi du-te pur aritmetică.

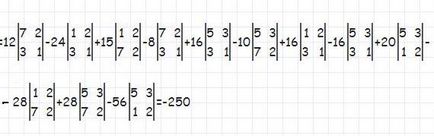
Expansiunea în coloană / rând - aceasta este doar una dintre modalitățile de a calcula determinantul unei matrice.

Este ușor de a verifica cantitatea de finali polinoame, se calculează factorialul numărului de coloane \ rânduri ale matricei. Deci, pentru matricea noastră finală de ordinul 4 polinomului trebuie să fie de 4! = 24 bucăți.

Dacă matrice are zero elemente, este recomandabil să se stabilească pe coloana sau rândul care conține cât mai multe zerouri posibil. Este evident că, cu unii minori suplimentare vor fi multiplicate cu zero și nu pot fi calculate.

• Găsirea determinantul metodei de descompunere matrice pe rând / coloană