Munca și puterea de forță - concepte de bază și definiții

Munca unei forțe constante pe o secțiune dreaptă

Să considerăm punctul materialul M căruia o forță F. Presupunem că punctul sa deplasat din poziția în poziția M0 M1. drumul său s (fig. 1).

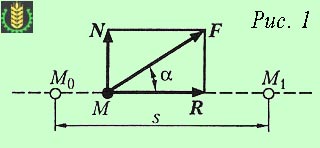
Pentru a stabili o măsură cantitativă a forței de impact F pe modul în care s. extinde forța asupra componentelor N și R. respectiv îndreptate perpendicular pe direcția de deplasare, și de-a lungul acesteia. Deoarece componenta N (perpendicular deplasare) nu se poate deplasa punctul sau să reziste mișcării sale în direcția s. atunci acțiunea forței F s pe drum, puteți defini produsul de Rs.
Această valoare se numește lucrarea și este notat W.
Prin urmare,

W = Rs = Fs cos α.

t. e. forța de muncă este produsul calea modulului său și cosinusul unghiului dintre direcția vectorului forței și direcția de mișcare a punctului material.

Astfel, lucrarea este o măsură a forței aplicate materialului la un anumit punct este mutat.
Munca este o cantitate scalară.

Având în vedere forța de muncă, există trei cazuri speciale: forța este direcționată de-a lungul deplasării (α = 0˚). forța este îndreptată în direcția opusă mișcării (α = 180˚). și forța de deplasare perpendiculară (α = 90˚).
Pe baza mărimii cosinusul unghiului a. se poate concluziona că, în primul caz, operațiunea este pozitiv, al doilea - negativ, iar în al treilea caz (cos 90˚ = 0) forța de muncă este zero.
De exemplu, mișcarea corp de funcționare gravitațională în jos este pozitiv (forță vector coincide cu mișcarea), la ridicarea caroseriei a forței de gravitație va fi negativ, în timp ce corpul în mișcare orizontală în raport cu suprafața de lucru a gravității pământ va fi egal cu zero.

Forța de aderență, lucru pozitiv, denumit în continuare forțele în mișcare. forțe, și se angajează operațiune negativă - forțele de rezistență.

Unitatea de lucru adoptat de Joule (J):
1 J = forța x x lungime = Newtonmetru = 1 Nm.

Joel - o forță de muncă de un newton pe drumul spre un metru.

Forța de muncă în secțiunea de cale în curbă

Pe DS zona infinitezimale traseu curbat poate fi considerată în mod convențional ca simplă și rezistență - constantă.
Apoi elementare de lucru forța dW pe DS cale este

dW = F ds cos (F. v).

Lucrările la deplasarea finală este suma lucrărilor elementare:

cos W = ∫ F (F. v) ds.

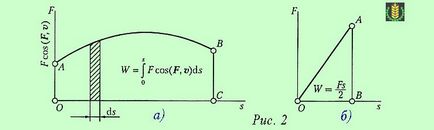
Figura 2a prezintă un grafic al relației dintre distanța parcursă și cos F (F. v). Zona benzilor umbrite un infinitezimale DS de deplasare poate fi luată ca un dreptunghi, este o lucrare elementară pe DS cale:

cos dW = F (F. v) ds,

și activitatea forței F pe calea lungă s este exprimată grafic cifrele OABC zona. axa abscisă Limited, și două ordonate ale curbei AB. care se numește curba forțelor.

Dacă lucrarea coincide cu direcția de deplasare și crește de la zero în raport cu traiectoria, operația este exprimată grafic zona triunghi BAW (Fig. 2 b). care, după cum se știe, se poate determina pe jumătate înălțimea de bază a produsului, adică jumătate lucrări de forță pe calea ..:

Teorema asupra rezultantei

Teorema: activitatea forțelor rezultante ale sistemului într-o anumită secțiune a traseului este suma algebrică a componentelor forței de muncă de pe aceeași porțiune de drum.

Lăsați un punct material M este sistem de forțe (F1. F2. F3. Fn) aplicat. care este rezultanta FΣ (fig. 3).

Sistemul de forțe aplicate pe un punct material, există un sistem de forțe convergente, prin urmare,

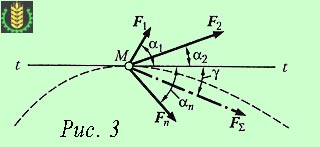
Noi proiect vectorul este egal cu tangenta la calea urmată de punctul de material în mișcare, atunci:

Inmultiti ambele părți cu un DS de deplasare infinitezimale și integrarea ecuației rezultată în cadrul unor deplasări finită s:

care corespunde ecuației:

Teorema privind forța de gravitație

Teorema: activitatea de gravitație este independentă de calea și este egală cu produsul dintre modulul de alimentare pe deplasarea verticală a punctului său de aplicare.

Lăsați materialul se deplasează punctul M sub forța gravitației G și pentru o anumită perioadă de timp, se mută de la poziția la M1 M2. drumul său s (Fig. 4).

Pe traiectoria M selectați DS porțiune infinitezimale. care poate fi privit ca o linie dreaptă, și din toate desena linii drepte paralele cu axele de coordonate, una verticală și cealaltă pe orizontală.
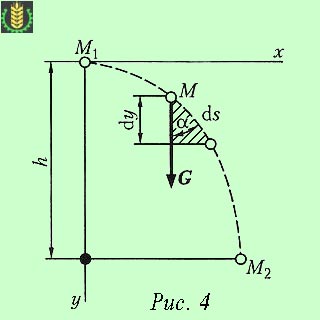
Din triunghiul umbrit, constatăm că

Lucrarea elementară a forței G de pe ds cale este egală cu:

Forța de muncă totală de greutate G este pe modul în care s

W = ∫ α = cos Gds ∫ gdy = G = ∫ dy Gh.

Astfel, activitatea forței gravitaționale este egală cu produsul dintre forța asupra deplasării pe verticală a punctului său de aplicare:

Un exemplu de rezolvare a problemei definirii forței de muncă de gravitație

Sarcina: O uniformă dreptunghiular matrice ABCD masa m = 4080 kg are dimensiunile prezentate în Fig. 5.

Determina operație trebuie efectuată pentru înclinarea în jurul unei muchii de matrice D.

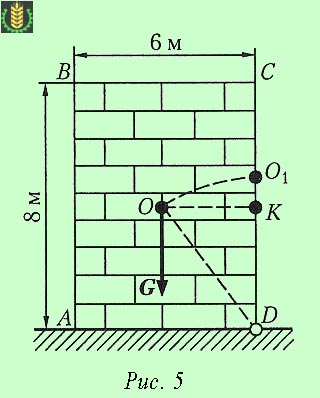
Decizie.
Evident, munca necesară este egală cu rezistența care se realizează prin gravitație o matrice, în care deplasarea verticală a centrului de greutate al matrice prin muchia de răsturnare D este calea care determină mărimea forței gravitațională.

Pentru a începe, definim forța de gravitație a șirului: G = mg = 4080 x 9,81 = 40 000 N = 40 kN.

Pentru a determina deplasarea verticală a centrului de greutate h uniformă matrice dreptunghiulară (situată în punctul de intersecție al diagonalelor dreptunghiului), folosind teorema lui Pitagora pe baza cărora:

KO1 = OD - KD = √ (KD OK 2 + 2) - KD = √ (3 Feb. 2 4) - 1 = 4 m.

Pe baza teoremei privind gravitatea defini lucrările necesare necesare pentru înclinarea matrice:

W = G × KO1 = 40 000 x 1 = 40 000 J = 40 kJ.

De lucru forță constantă aplicată corpului rotativ

Imaginați-vă un disc rotativ în jurul unei axe fixe la o forță F constantă (Fig. 6). punctul aplicare care se deplasează împreună cu discul. Noi extindem forța F pe trei componente reciproc perpendiculare: F1 - forță circumferențială, F2 - forță axială, F3 - forță radială.

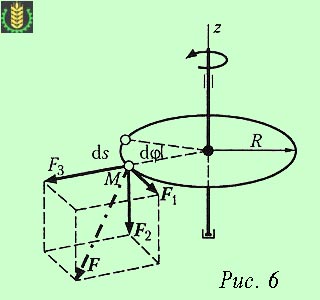
Când se rotește butonul de pe unghiul infinitezimal dφ forța F va face munca elementar, care pe baza teoremei lucrării rezultat va fi egală cu suma lucrărilor componentelor.

Este evident că activitatea componentelor F2 și F3 este zero, deoarece vectorii acestor forțe sunt perpendiculare pe punctul de aplicare ds deplasarea infinitezimal M. Prin urmare, activitatea elementară a forței F este egală cu F1 sale componente:

Atunci când cadranul este rotit la unghiul cp final este lucrarea forței F

în care unghiul cp este exprimat în radiani.

Deoarece momentele componente F2 și F3 în raport cu axa z sunt egale cu zero, pe moment, teorema bază Varignon a forței F în raport cu axa z este:

Momentul de forță aplicată pe disc, axa de rotație se numește un cuplu, și, în conformitate cu standardul ISO. notate cu litera T.

T = Mz (F). De aceea, W = Tφ.

De lucru forță constantă aplicată unui corp rotativ, este produsul cuplului pentru deplasarea unghiulară.

Un exemplu de rezolvare a problemei

Obiectiv: mânerul de acționare rotește forța vinci F = 200 N perpendicular pe raza de rotație.
Găsi de lucru consumat în timpul t = 25 de secunde. dacă lungimea brațului r = 0,4 m. și ei viteza unghiulară ω = π / 3 rad / s.

Decizie.
În primul rând, definirea unghiulară mânerul de deplasare φ troliu timp de 25 de secunde:

φ = ωt = (π / 3) × 25 = 26,18 rad.

În continuare, vom folosi formula pentru determinarea forței de funcționare în timpul mișcării de rotație:

W = Tφ = Frφ = 200 x 0,4 x 26,18 ≈ 2100 ≈ 2,1 J. kJ.

Munca efectuată de către o forță care poate fi pentru diferite perioade de timp, adică. E. La viteze diferite. Pentru a caracteriza modul în care munca se face rapid, există un concept in mecanica a puterii. care este de obicei notată cu litera P.

Puterea se numește activitatea desfășurată pe unitatea de timp.

Dacă lucrarea se face în mod uniform, puterea este determinată prin formula

Dacă direcția forței și direcția de mișcare a fel, că această formulă poate fi scrisă într-o altă formă:

P = W / t = Fs / t sau P = Fv.

forța de alimentare este produsul modulului de alimentare de pe viteza punctului său de aplicare.

Dacă operația este realizată printr-o forță aplicată uniform pe corpul rotativ, puterea în acest caz, poate fi definită prin formula:

P = W / t = Tφ / t sau P = Tω.

Puterea de forța aplicată unui corp uniform prin rotație este produsul cuplului prin intermediul vitezei unghiulare.

Unitatea de măsură este de wați de ieșire (W):

W = munca / timp = joule pe secundă.

Conceptul de eficiență energetică și

Capacitatea corpului în timpul tranziției de la un stat la altul pentru a face munca este numită energie. Energia este măsura comună a diferitelor forme de mișcare a materiei.

Mecanicii pentru conversia de transfer și de energie sunt diverse mecanisme și mașini, scopul care - punerea în aplicare a persoanei specificate de caracteristici utile. În acest caz, energia transferată la un mecanism numit de energie mecanică. care este fundamental diferită de formele termice, electrice, electromagnetice, nucleare și alte bine-cunoscute de energie. Tipuri de energie mecanică a corpului, ne uităm la pagina următoare. dar aici definesc numai conceptele de bază și definițiile.

Atunci când transferul sau de conversie a energiei, precum și atunci când se face la locul de muncă au pierderi de energie, deoarece mașinile-unelte și servesc pentru a transfera sau de a transforma forța de energie a depăși diferite de rezistență (mediul înconjurător rezistența la frecare și așa mai departe. P.). Din acest motiv, atunci când transferul o parte din energie este pierdută și nu poate fi utilizat pentru a efectua o muncă utilă.

Eficiența

O parte din energia pierdută în timpul transmisiei pentru a depăși forțele de rezistență, a reprezentat pentru utilizarea eficienta a mecanismului (mașină), care transmite această energie.
Eficiența (COP) este notat cu η și este definit ca raportul dintre lucrul mecanic util (sau putere) consumate la:

În cazul în care eficiența pierderilor mecanice ia în considerare numai, se numește randamentul mecanic.

Este evident că eficiența - întotdeauna o fracțiune corespunzătoare (uneori, exprimată în procente) și valoarea sa nu poate fi mai mare decât unul. Mai aproape de unitatea valoarea eficienței (100%). aparatul de rulare economică.

În cazul în care energia sau puterea transmisa urmatorul mecanism secvențial, eficiența totală poate fi definită ca produsul tuturor eficienței mecanismelor: